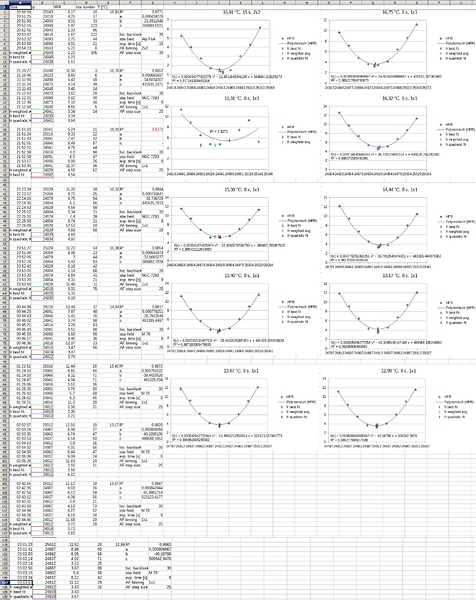
When trying the AF routine of SGP I was intrigued by the fact that I didn’t get “V-shaped” curves but nice parabolas. So I examined the results of all 19 AF runs of three nights (20., 27. and 31. of october) with different observing conditions more strictly. I want to share my results and my conclusion:
Used equipment:
I am using a Takahashi FSQ 106N (focal length 530 mm, aperture 106 mm) which is notorious for a strong focus drift with temperature (it is about -50 µm/K). My scope has the original rack & pinion focuser which has been carefully adjusted by Rèmy at Optique Unterlinden in Colmar. The focuser has no reduction gear. The attachment of the motor to the scope is constructed solidly in order to avoid distortion of the motor shaft which would result in lateral forces to the focuser shaft. The motor is connected to the focuser shaft by a Flexible Shaft Coupling. A Robofocus motor (3600 steps/revolution) and Seletek Armadillo2 controller is used.
In SGP a focuser backlash of 30 steps, direction IN was set. For the AF runs, the number of Data Points was always set to 9, the step size to 17 (= 113 µm) as a starting point. Later on I raised the step size to 25 (= 167 µm) which worked very well. With an even higher step size SGP didn’t detect stars when out of focus.
Evaluation:
I examined the results of the AF runs by retrieving the following data from the logfiles: focuser positions (fp), HFR values and the focus results (fr) obtained by both “Weighted Average” (old) und “Best Fit” (new) SGP AF evaluation methods. The data of each focus run (HFR vs. fp and fr) were analysed and plotted in a spreadsheet software. A 2nd order polynome regression (“Quadratic Fit”) of each of the curves was applied which provided the coefficients a, b, c of the regression equation (1) and the coefficient of determination R^2 for each focus run:
HFR(fp) = afp^2 + bfp + c (1)
1st derivative:
HFR’(fp) = 2afp + b
The condition for the minimum of the function (HFR’(fp) = 0) provides:
fr = -b/2a (fr is the fp at the minimum of the regression curve) and
HFRmin = -(b^2/4a) + c (HFRmin is HFR at the minimum of the regression curve)
The regression equation (1) thus can be transformed to a different representation (2):
HFR(fp) = a*(fp - fr)^2 + HFRmin (2)
For decent (16 of 19) AF runs the “Quadratic Fit” was very good, R^2 being in the range of 0.960 to 0.997, in most cases between 0.975 and 0.997 (images 1 to 3). 3 AF runs were poor, with R^2 of 0.527, 0.241 and 0.095 respectively. Two of the poor AF runs were influenced by the bad conditions in the second night, when thin clouds came up. At the third poor AF run the very first HFR value deviated heavily from the expected value.
With the “Quadratic Fit” method I determined the fr values (= focus position at the minimum of the regression curves) for all AF runs and compared them with the results of SGP’s AF evaluation methods. Then I plotted the focus result values (fr) vs. temperature (T) separately for SGP’s AF evaluation methods and the “Quadratic Fit” method. For the sake of comparability in all three plots only the 16 AF runs were included which exhibited a R^2 > 0.95 in the quadratic fit. For the fr vs. T plots (temperature dependency) a linear regression was applied (image 4).
Assessment:
The comparison of these data shows that the “Quadratic Fit” method has important advantages compared to both of SGP’s AF evaluation methods:
-
Distinct identification of poor AF runs
There is a numeric criterion for the quality of an AF run: the coefficient of determination of the quadratic regression curve (R^2). This allows for the AUTOMATIC exclusion and repetition of poor AF runs. However, the exclusion of poor AF runs based on SGP’s AF evaluation methods seems not to be automatable and is highly subjective. -
Robustness against a single outlier of a HFR value
The “Quadratic Fit” method uses all of the focus shots, in the evaluated AF runs that means there are 9 points for the regression. As a result the fr value are little influenced by a single outlier of a HFR value, i. e. the “Quadratic Fit” method is accurate and robust. In contrast SGP’s “Best Fit” method is strongly disturbed by a single outlier of a HFR value at the edge of a curve, and the “Weighted Average” method indeed is robust, but suffers from coarsely graded fr values. For this reason one can expect also a higher precision of the fr values obtained by the “Quadratic Fit” method. -
Correlation of fr values with temperature
When comparing the plots of the focus result values (fr) vs. temperature (T), in the linear regression the “Quadratic Fit” method exhibited significantly higher R^2 compared with the two SGP AF evaluation methods. The correlation of the fr values obtained by the “Quadratic Fit” method with temperature was significantly higher than that of SGP’s methods (see image 4).
My conclusion is that the results of the “Quadratic Fit” method are more reliable than those of SGP’s AF evaluation methods. Therefore I propose to implement this method for the evaluation of AF results.
Bernd
I think that’s rather a matter of effort than of skill, but yes: if someone using a different scope/camera combination than I provided a logfile, I would do that evaluation.