We are testing a proposed new routine for determining the best possible focus position that each auto-focus run determines.
This routine is fully programmed and has already been run against 1000+ focus runs. The results from these runs show major improvements over the routine currently implemented in SGP.
But the 1000+ runs only encompass logs from 4 different users. It does include both Newtonians and refractors with both long and short focal lengths.
The improved results are very exciting, however, we need logs from many more users, particularly users that have been having difficulties with the current routine.
========== Please send us your logs ===========
Send logs through this forum as a download link, or directly to me at jerry@maconsys.com
If you send me your logs, I will send you back a text file detailing what this method would produce for your focus positions.
Who are we?
@bulrichl orginally started this project two years ago with his excellent presentation of the potential of the Quadratic focus fitting using LibreOffice. See “Proposal of a “Quadratic Fit” Auto Focus evaluation method”. He is programming LibreOffice to be able to output our vast collection of V curves on the same graph as the derived Quadratic curve, and thereby help us refine our logic code.
@mikaelA has created the “SGP AutoFocus LogViewer”, a fabulous program free to us all, that reads SGP log files and outputs wonderful plots of all the focus run V curves, and a linear plot of the best fit Temperaure line for the night’s focus runs. Now a special version of this outputs all the V curve data points into a TXT file that my program reads to determine the best Quadratic fit. Without this we could not process and analyze hundreds of focus runs in a reasonable period of time.
@jmacon I have programmed the Quadratic best fit routine in C++. That actually turned out to be quite easy, it is only about 60 lines of code. The more extensive effort has been programming the input of the data, and the output of analysis reports. The really time consuming part comes next, when you have sent us your logs and we analyze them in detail to make sure our code is coming up with the best possible focus values.
The program sequence we have developed allows us to process hundreds of Log files very quickly, and produce both summary and detail reports.
I should be clear on what it does and does not do.
A simple outline of what the SGP auto focus routine does is:
- take images over a range of focus positions surrounding the current focus position
- find stars and calculate their HFR in each image
- from this collection of Position-HFR data points, plot the V curve
- given the V curve data points, determine the best focus position (2 methods used)
- [FUTURE] allow a rerun of the focus run if some Quality Metric is not met
Our Quadratic focus routine only deals directly with 4) and 5). Basically 2), 4) and 5) are the steps where improvements can be made. Ken has indicated that 5) will be included in the current SGP release. I expect the Quadratic routine will make some improvement in 2), for those users where star detection is causing the problems. I expect this improvement because the V curves for those people are of a lower quality and therefore exactly the class of V curves for which our routine makes significant improvements. However, the major improvements in difficult star detection can only be made by the developers addressing 2).
The Quadratic routine provides the following two major improvements:
- provides a perfect Quality Metric (R^2) that the developers will need for implementing 5) above.
- gives a much better value for Best Focus Position for V curves that are less than ideal.
To be clear, the Quadratic and SGP give basically identical results for good V curves, which comprise the vast majority of all V curves produced by the SGP user base. Where Quadratic really shines is that small percentage (for most people) of focus runs that are not good V curves. My night’s run on July 17 provides good examples.
Here are all 8 focus runs on July 17 with my 12" Newtonian, an AG12 from Orion Optics, which show clearly where the Quadratic routine gives much better results. This scope/camera runs at .70 arcsecond resolution which increases the likelihood of difficult focus runs compared to larger resolutions.
NOTE: The letter S shows best focus position determined by SGP.
The letter Q shows best focus position determined by the Quadratic routine.
(the vertical position of the letter is meaningless, just its position along the horizontal (POSITION) axis indicates the best focus position)
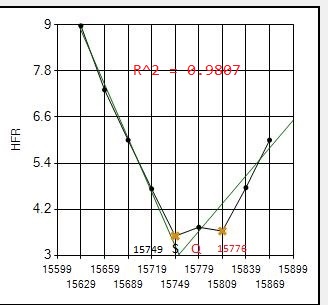
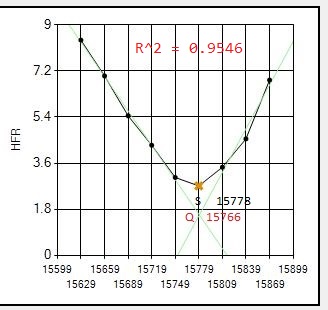
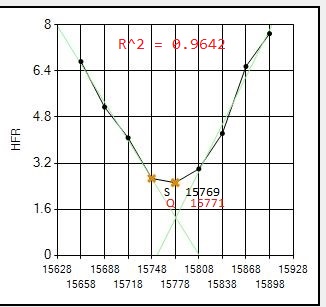
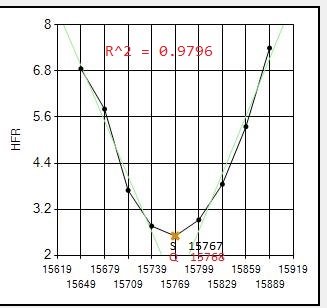

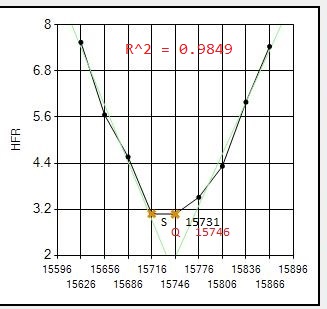
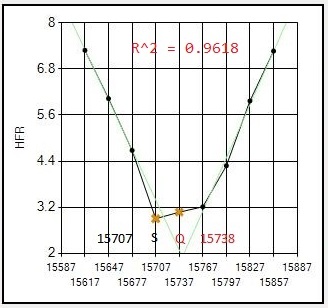
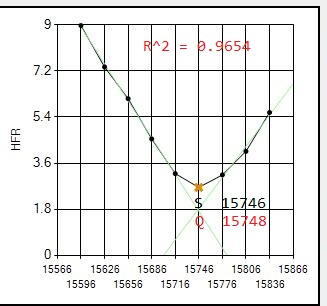
Note that out of the 8 focus runs that night, the Quadratic routine significantly improved focus for 3: #1,#6,#7. All 8 focus runs gave quality metric R^2 values > 0.96 so no reruns were required.
We have more proof this Quadratic fit method makes important focus improvements. Yes, it made much better choices for 3 out of 8 of my focus runs. But were they really improvements in actual focus? Here are the Temperature vs Focus Position plots for SGP compared to Quadratic:
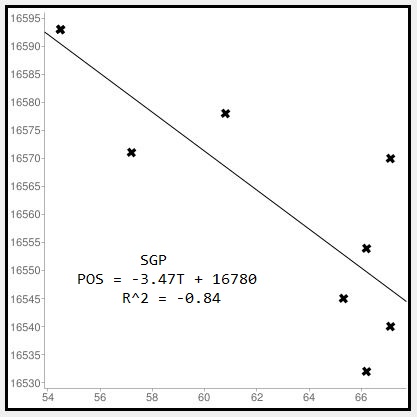
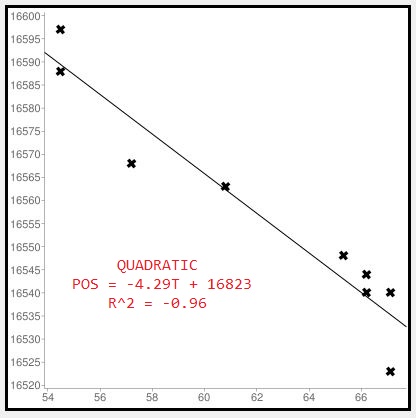
Major improvement in R^2 from .84 for SGP, to .96 for Quadratic. The fit of the least squares fit line is obviously much better, so we have a real improvement in focus positions.
Here are examples of focus curves with poor quality metric R^2 values that would trigger a rerun.
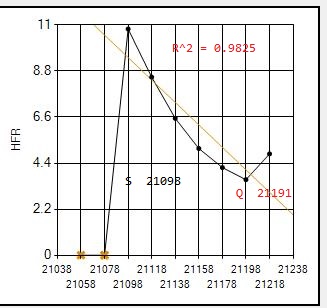
This is unfortunately a very common example where the starting focus point was so far out of focus that the last two images could not detect any stars and gave hfr=0. the SGP selected best focus point was actually at the worst possible focus. Quadratic actually made this an acceptable run with R^2=0.9825 because it threw the two 0 points away and only used the others, which form a very lop-sided V curve but otherwise a good quadratic fit. So the best focus quadratic returned was useable. However, in this situation we would probably want to trigger a rerun and also return a new starting focus position so that the rerun would be centered.
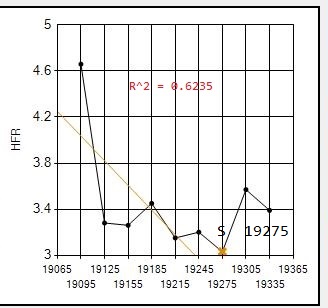
This is a fairly typical example of simply a poor focus run that more or less resembles the correct curve, but really warrants a rerun. The actual best focus based on the excellent focus runs on each side of it was at 19240, more than one full step increment away from the SGP value of 19275. Quadratic gives us R^2 = 0.6235 clearly triggering a rerun.
The Quadratic routine handles special cases well, like this example where one data point is really bad, but the rest of the points make a really good V curve. SGP does fine with this run.

Summary of results from our initial 1000+ focus runs:
The R^2 values are very effective in distinquishing betweeen good/excellent runs, and poor runs that warrant a rerun.
R^2 from .94 to 1.0 —> always excellent runs
R^2 from .90 to .94 —> somewhat choppy runs but usually very useable
R^2 from .75 to .90 —> very few fall in this range
R^2 from 0 to .75 —> really bad runs that require a rerun
Please note: R^2 has proven to be very effective in determining the key thing we want to use it for, deciding whether or not to perform a rerun. The user choice of where to set the break point is not a critical or sensitive point. Anything between .8 and .9 is likely to work just fine.
Hopefully with many more logs from users and much more testing, we will have this to the point where Ken and Jarod and the user base will be convinced of its effectiveness and will proceed to implement it. We will provide all the code to the developers. The quadratic routine is small and well packaged and should be straight forward to implement.
Additional suggestions for improvement are certainly welcome.